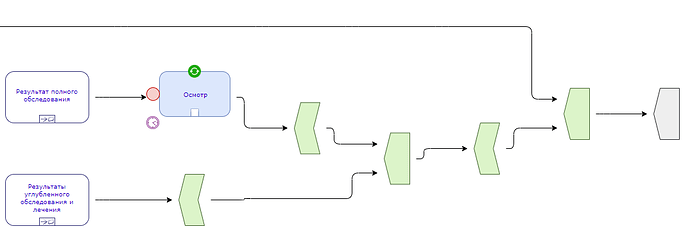
Here’s a typical example of the ‘end-block’ problem we get in current Task Planning visual modelling language (VML):
In the current version of things, every end-block has a visual node, as shown above. This makes for a ‘long-tail’ problem visually. If we were programming, it would be like a series of end -’}’, finally getting to the outermost level.
So to fix it, the first approach I’d like to try is not to change the formal structure (which I am not opposed to, but that’s harder and we need to be very careful, for obvious reasons) - but instead to define a ?simple algorithm for drawing tools that will collapse these long tails.
Remembering that each of those end-block icons is a TASK_GROUP (or CHOICE_GROUP, … etc) join point, where all the paths started in that same TASK_GROUP now have to join back.
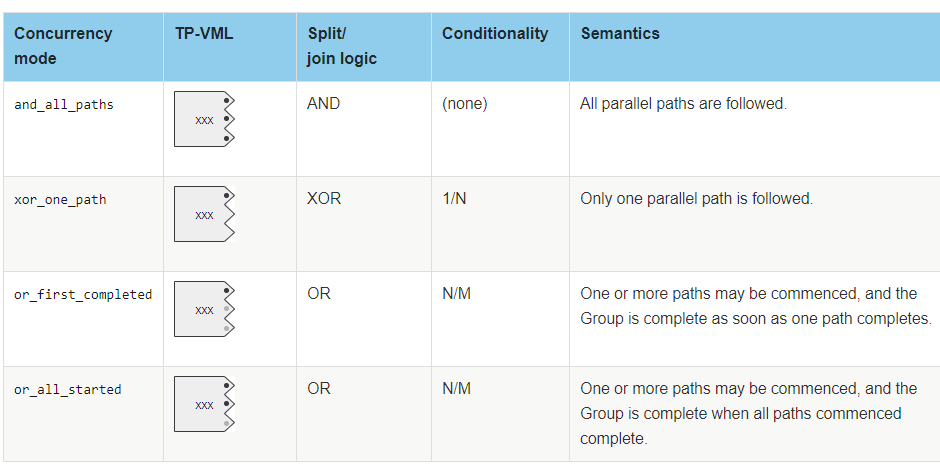
For a TASK_GROUP to ‘complete’, such that execution can move beyond, the rules of that Group’s completion have to be obeyed. At the moment, we have the following varieties of TASK_GROUP:
For the CHOICE_GROUPs, the logic is always xor_one_path.
Now, in many cases, the TASK_GROUP contents are sequential, and there is only one entry line into the end-group box. So as soon as execution gets there on that one path, the Group is complete, and execution can keep going, no waiting.
So the real problem is in cases with multiple entry paths into an end-block.
Based on the table above, the logic at each such block point will be one of:
wait till all paths arrive = AND-JOIN
wait till first path arrives = XOR-JOIN
wait till first path completes = OR-JOIN variant 'first complete'
wait till all paths started at time of first completed path arrive = OR-JOIN variant 'all started'
Visually he problem is that multiple paths are ganged together according to their original Group SPLIT points (the start of the block), so we can’t just join all those lines together.
However, single sequential paths can be collapsed, and I think XOR-JOIN paths as well, since it’s the same logic.
However, AND-JOIN and OR-JOIN blocks can’t be erased, but there’s no reason not to try for a less visually inefficient approach. YAWL and van der Aalst’s preceding research on Petri nets is a place to look. I have some ideas, but it’ll take a bit of time to draw them out.
I will note that the biggest challenge of this type in YAWL is indeed the OR-JOIN point, just as it is here - both for trying a visual collapsing strategy, and for allowing freer use of join points as Fabio@Better would like.
Anyway, one thing at a time… before we get there, do we all agree on the above analysis?